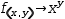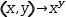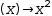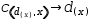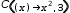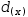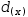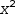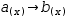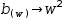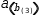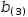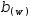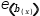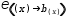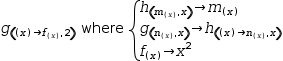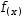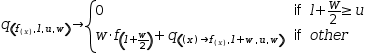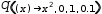9.6 Lambda Expressions
A lambda expression is an anonymous function definition to which a function
parameter with the same signature can be bound.
To create a lambda expression, the lambda symbol is used in place of a function name. That is,
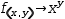 f(x, y)→x^y as an anonymous definition is written λ(x,y)→x^y.
The display form of a lambda expression simply omits the function name:
f(x, y)→x^y as an anonymous definition is written λ(x,y)→x^y.
The display form of a lambda expression simply omits the function name: 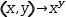 λ(x, y)→x^y.
An alternate syntax for single-parameter
lambda expressions omits the parameter parenthesis. That is,
λ(x, y)→x^y.
An alternate syntax for single-parameter
lambda expressions omits the parameter parenthesis. That is, 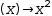 λ(x)→x^2 can
be entered as λx→x^2.
λ(x)→x^2 can
be entered as λx→x^2.
Lambda expressions must be typed; this example elaborates a set:  λʂ(x)→{log(2, x), x^2}
but note the non-real function-type, normally indicated by a bold-face non-serif function name,
is missing in the displayed form along with the function name. Inspection of the text-output area reveals
the typed form: λʂx→{log(2,x),x^2}.
λʂ(x)→{log(2, x), x^2}
but note the non-real function-type, normally indicated by a bold-face non-serif function name,
is missing in the displayed form along with the function name. Inspection of the text-output area reveals
the typed form: λʂx→{log(2,x),x^2}.
Like any other expression, a standalone lambda expression can be evaluated
by providing arguments. It is not usually useful, but (λx→x^2)(3)
– which is automatically generated from (x^2)(3)
and displays the same as (f(x)→x^2)(3) – can be evaluated.
But as mentioned above, a lambda expression can be passed, unevaluated, as a parameter to a function.
In the latter's elaboration,
the function parameter can be evaluated or passed on, unevaluated.
To see this in action,
consider the definition 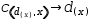 c(d(x), x)→d(x) and the evaluation of
c(d(x), x)→d(x) and the evaluation of 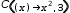 c(λ(x)→x^2, 3).
During activation, formal parameter
c(λ(x)→x^2, 3).
During activation, formal parameter 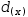 d(x) is bound to the lambda expression and
formal parameter x is bound to 3.
In the elaboration of c,
d(x) is bound to the lambda expression and
formal parameter x is bound to 3.
In the elaboration of c, 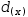 d(x) is evaluated as
d(x) is evaluated as 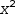 x^2.
Contrast this with the definitions
x^2.
Contrast this with the definitions 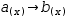 a(x)→b(x) and
a(x)→b(x) and 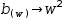 b(w)→w^2 along with the evaluation of
b(w)→w^2 along with the evaluation of
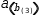 a(b(3)). Here, a is passed the real result of
a(b(3)). Here, a is passed the real result of 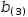 b(3),
as evaluated by the non-local
b(3),
as evaluated by the non-local 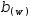 b(w).
b(w).
Three questions arise: how does a function expression in an elaboration
know to be bound directly or via a function parameter?
what determines whether a function will be passed or evaluated?
and how can a function already defined be passed as a parameter.
The answer to the first question is a matter of scope and the observation that the scope of
an elaboration is nested within the scope of the function's parameters and that within the workspace.
Thus, a function expression
will be bound to a function parameter, or to a function in the workspace, or binding will fail.
If bound to a function parameter, the call chain will ultimately end in a lambda expression.
The second question is answered by noticing whether a lambda expression is used. The two
expressions 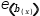 e(b(x)) (in which b is invoked) and
e(b(x)) (in which b is invoked) and 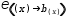 e(λ(x)→b(x)), (in which b is passed
as a parameter) have a different appearance.
e(λ(x)→b(x)), (in which b is passed
as a parameter) have a different appearance.
To answer the third question, consider the serial tuple
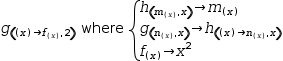 (h(m(x), x)→m(x), g(n(x), x)→h(λ(x)→n(x), x), f(x)→x^2, g(λ(x)→f(x), 2)).
(h(m(x), x)→m(x), g(n(x), x)→h(λ(x)→n(x), x), f(x)→x^2, g(λ(x)→f(x), 2)).
Working from right to left,
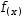 f(x)
f(x) is passed as a lambda expression to function
g, which passes it in turn
to function
h using another lambda expression.
9.6.1 Quadrature, revisited
Using quadrature, the definite integral of a function is computed numerically.
The implementation in §9.3.5 binds the quadrature algorithm to a non-local function.
The function-parameter version of this is realized as
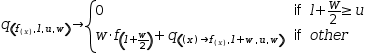 q(f(x), l, u, w)→l+w÷2≥u?0:w⋅f(l+w÷2)+q(λ(x)→f(x), l+w, u, w).
q(f(x), l, u, w)→l+w÷2≥u?0:w⋅f(l+w÷2)+q(λ(x)→f(x), l+w, u, w).
Now
q can be evaluated using
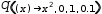 q(λ(x)→x^2, 0, 1, 0.1)
q(λ(x)→x^2, 0, 1, 0.1).